что для построения графика знак
Пример 7
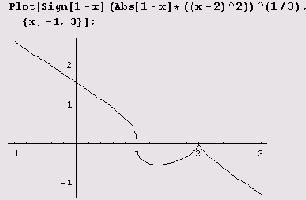
Заметьте, что для построения графика знак подкоренного выражения пришлось вынести из под корня, благодаря чему подкоренное выражение оказалось неотрицательным.
Нахождение наибольшего и наименьшего значений (глобальных экстремумов)
Если область определения дифференцируемой функции состоит из нескольких отрезков, то, чтобы найти ее глобальные экстремумы, можно сначала найти ее локальные экстремумы, а затем значения на концах отрезков. Из этих значений и нужно выбрать наибольшее и наименьшее. В общем, нет ничего сложного, если, конечно, все вышеперечисленные операции выполняются без проблем.
Нахождение интервалов выпуклости и точек перегиба
Найдем интервалы выпуклости и точек перегиба функции y2= х4-6х2—6х+1. Сначала введем функцию в систему Mathematica.
y2=x^4-6x^2-6x+1 1-6х-6х2 + х4
Теперь находим вторую производную.
D[y2,{x,2}] -12 + 12 х2
Так как вторая производная положительна при |x| >1, то (-?, -1) и (1, ?) — интервалы выпуклости вниз, а (-1, 1) — интервал выпуклости вверх. Поскольку в точках х = -1 и х = 1 функция меняет направление выпуклости, эти точки являются точками перегиба. Впрочем, в этом можно убедиться и иначе: третья производная
0[у2,{х,3}]/.х->1 24 0[у2,{х,3}]/.х->-1 -24
в этих точках отлична от 0.
Вот график функции