и есть условие устойчивости точки
Пример 10
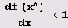
Это и есть условие устойчивости точки х*.
Будем дальше увеличивать параметр r. Поведение системы снова изменится: в последовательности {хn}, начиная с достаточно больших и, будут чередоваться числа, близкие к некоторым двум числам я, и а2. (Точнее говоря, последовательность устроена так, что x2n+1->a1, х2n+1->n2 при n->?) Эти числа связаны соотношениями а1 = f(а2), а2 = f(а1). Иными словами, в этом случае отображение хn+1 = rхn(1—хn) имеет устойчивый цикл с периодом 2. Обозначим этот цикл 52. Наличие цикла S* в нашей модели означает, что численность популяции будет меняться с периодом в 2 года.
Выясним, как выглядят циклы на графике. Для этого определим программу cobwebPlot.